Help Center

Configuration

Guides

Introduction to Calculated tags

Calculated input Group Logic

Calculated input is about setting up a calculation expression with one of more tags, like adding the readings from 2 tags together. In the following article, you will get an introduction to Calculated input groups.

Accessing the interface

Navigate to "DIAPs" and select it.

Choose the DIAP which you wish to add Calculated inputs for:

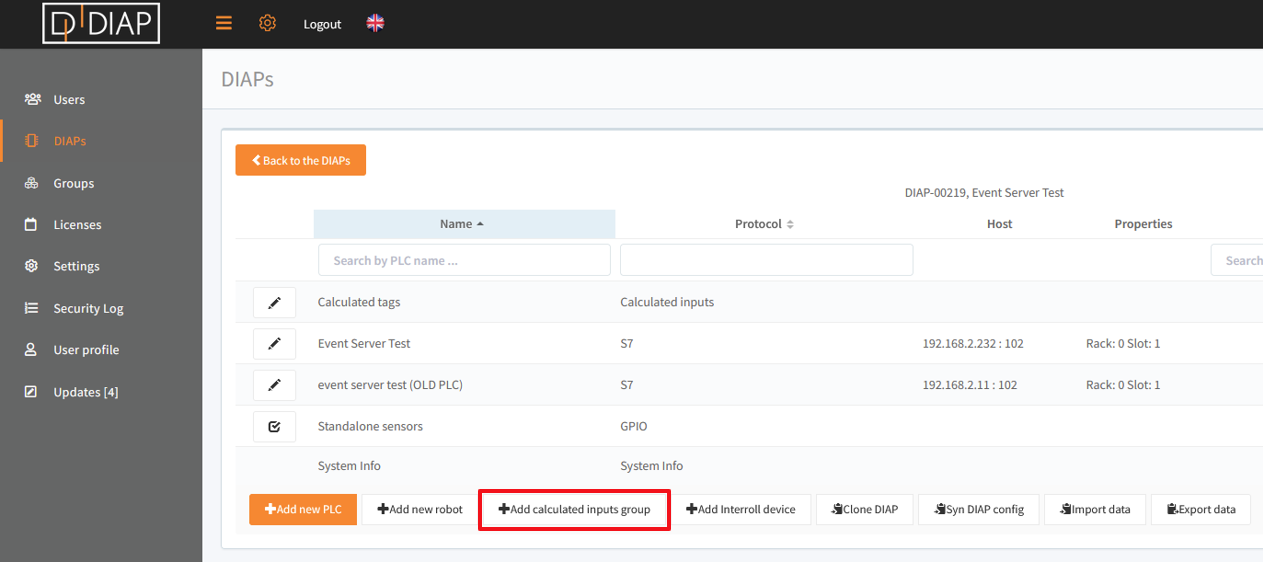
Choose the "+ Add calculated input group" in order to add a group for creating calculated tags. A calculated input group is basically a kind of virtual/software PLC, that can be setup and run inside the DIAP. It is a way for logical grouping a set of tags and it is needed to keep the relation between DIAP, tags' groups and tags.

A pop-up will occur:

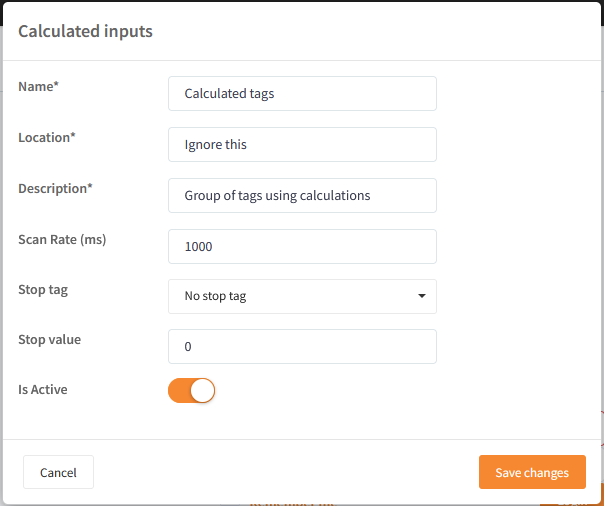
Name: The name of the calculated tags group (The virtual/software PLC)
Location: Just enter something here because this isn't used.
Description: A description of the calculated tags group.
Scan Rate (ms): The default scan rate, that will be used when adding a new input into this calculated tags group (This can be overwritten in the tag setting).
Stop tag: This setup is for when the tags in the group shouldn't collect data. Just set it to No stop tag, this will stop the tag from collecting data, when its reading is equal to that in the Stop value.
Stop value: This value is used to check if the tag shouldn't collect data.
Is Active: Sets the calculated tag group active or inactive. Tags in an inactive active group won't collect data.

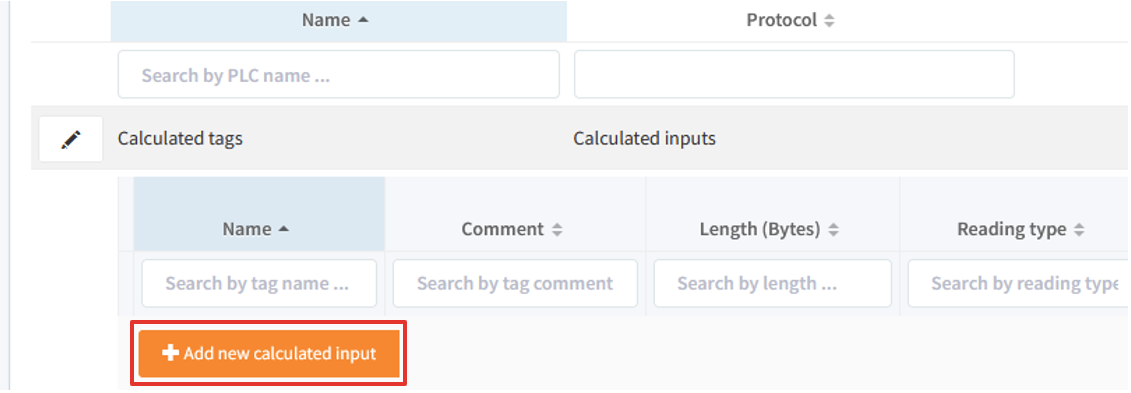
Once the group has been created, then it can be expanded in order to add new inputs. Click "Add calculated input".

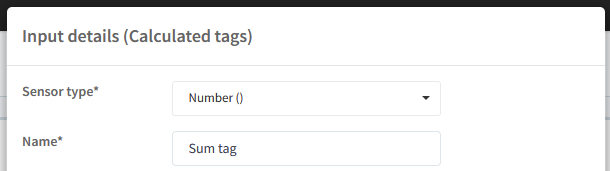
A calculated input is basically a tag, where one defines an expression to it, that will be calculated like a math formula. You must select a Sensor type, enter a Name for the calculated input:

Now you must specify the expression, that should be calculated, this expression most likely involves the use of other tags. To add a tag to the expression, click "Add new tag":

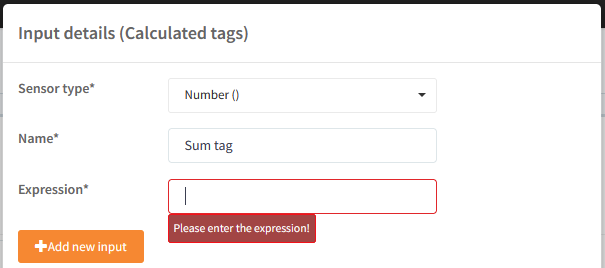
Press the button "+ Add new input" and select the PLC and tag.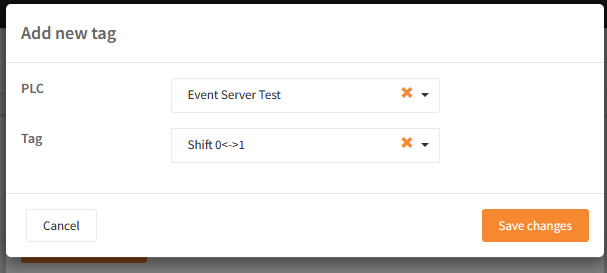

The added tag can now be seen in a list below: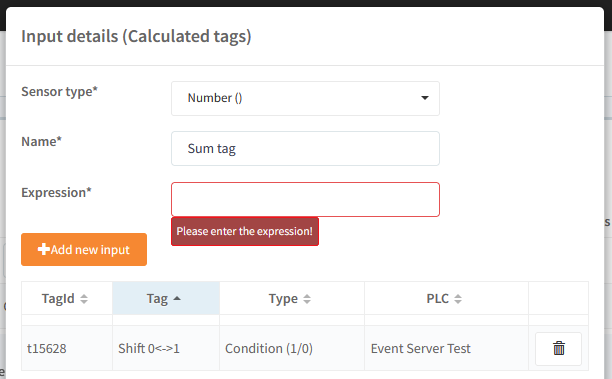

Repeat this for each tag needed in the expression.

To insert a tag into the expression, copy it's TagId, into the expression input: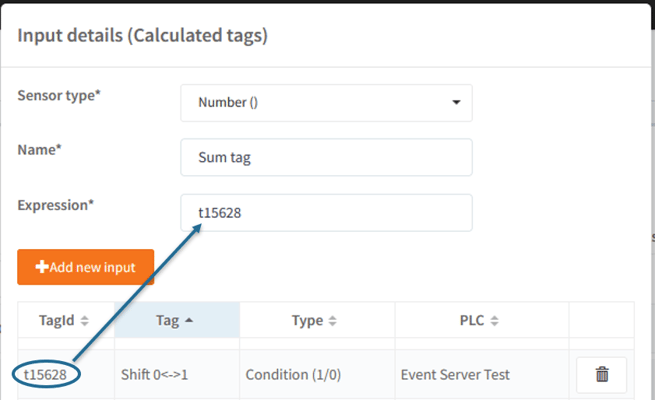

Here is an example of getting the sum of 2 tags, where Sum tag returns the sum of tag Shift 0<-> and irregular int: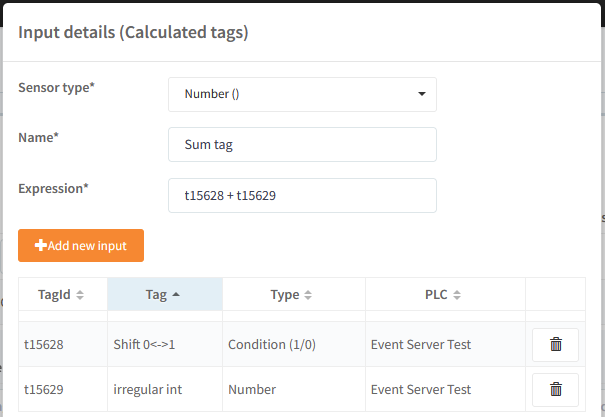

The rest of the settings for the calculated input are standard tag settings, which you can read more about here: Configuration of tags (PLC).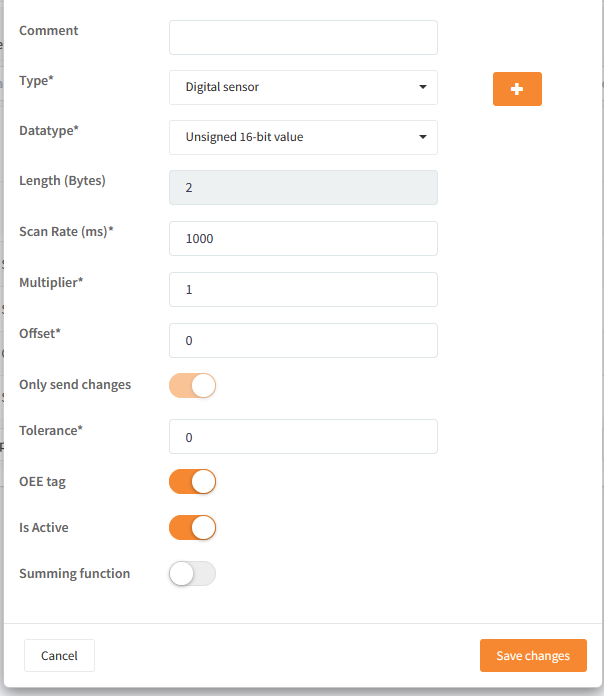

Basic usage examples

Here are some examples of use, using only three tags:

t997 - a simple boolean (can hold value 0 or 1).
t998 - a value between -127 and 128.
t999 - a simple boolean (can hold value 0 or 1) on another PLC.

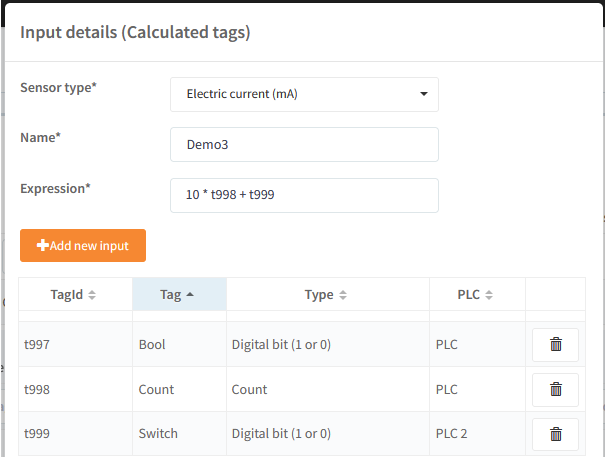
Mathematic:

Tags as shown above where:

t997 = 0
t998 = -3 
t999 = 1

Basic:

t999 + t997 = 1
t997 - t998 = 3
t999 / t998 = 1 / -3 = -0.3333~

Adding more complexity:

t998 * - t999 = 1 * - -3 = 3

Adding constants:

10 * t998 + t999 = 10 * -3 + 1 = -29

Adding parentheses:

10 * (t998 + t999) = 10 * (-3 + 1) = -20

Logic:

Tags as shown above where:

t997 = 0
t998 = 1
t999 = 1

Basics:

t997 & t998 = t997 and t998 = 0
t997 | t998  = t997 or t998  = 1

Negation:

not t997 = 1
not t998 = 0
not(t997 & t998)  = 1
not(t998 & t999)  = 0
not(t997 | t998)  = 0
not(t998 | t999)  = 0

"not(A & B)" acts as a NAND gate:

INPUT	INPUT	OUTPUT
A	B	A NAND B
0	0	1
0	1	1
1	0	1
1	1	0

"not(A | B)" acts as a NOR gate:

INPUT	INPUT	OUTPUT
A	B	A NOR B
0	0	1
0	1	0
1	0	0
1	1	0

The following logic operators can be used in the expression:

Logic operator	Description
&	Logic and operator
\|	Logic or operator
not(A & B)	NAND gate
not(A \| B)	NOR gate

Functions:

Tags as shown above where:

t997 = 0.7
t998 = 1.3
t999 = 2.3

You can use functions, like round, cos, acos, floor and others:

round(t999) = round(2.3) = 2

Combining them with math:

10 * round(t997) + floor(t998) + 10 = 10 * round(0.7) + floor(1.3) = 10* 1 + 1 = 12

You can only pass 1 parameter to the functions:

1 parameter (OK)

round(t997)

2 parameters (Not OK)

round(t997,2)

Functions

The following functions can be used in the expression:

Function	Description
acos	Returns the arc cosine of a number
asin	Returns the arc sine of a number
atan	Returns the arc tangent of a number in radians
atan2	Returns the arc tangent of y/x in radians
ceil	Rounds a number up to the nearest integer
cos	Returns the cosine of a number
cosh	Returns the hyperbolic cosine of a number
exp	Returns E raised to the power of x
fabs	Returns the absolute value of a number
floor	Rounds a number down to the nearest integer
log	Returns the natural logarithm of a number, or the logarithm of number to base
log10	Returns the base-10 logarithm of x
sin	Returns the sine of a number
sinh	Returns the hyperbolic sine of a number
sqrt	Returns the square root of a number
tan	Returns the tangent of a number
tanh	Returns the hyperbolic tangent of a number
bool	Returns the boolean value of the specified object
int	Returns an integer number
round	Rounds a number
random	Returns a random float number between 0 and 1 (Don't take a parameter, like this random())
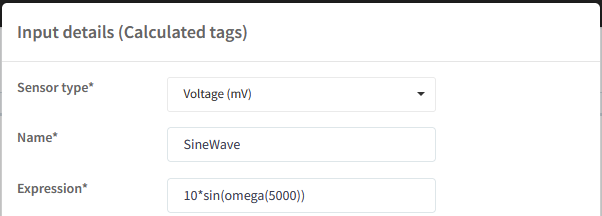
omega	omega(X) - is a function that emulates periodical events and with given rotational speed expressed as a period of 1 rotation per X ms, returns angle that can be used in trigonometric functions as an input parameter. Example: Sine wave = amplitude * sin(omega(period of wave expressed in ms))

Example of using omega:

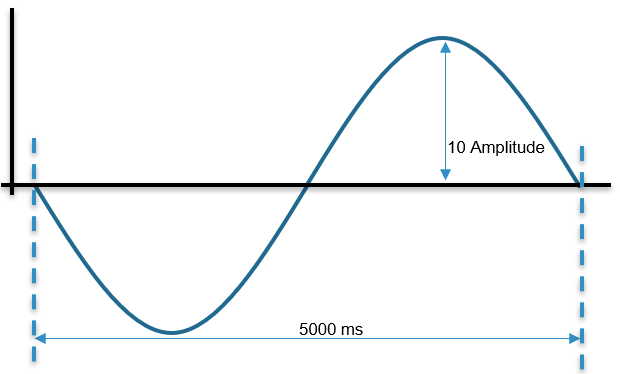
Then the calculated input will generate a sine wave like this:

Test expression

The expression is evaluated with python by passing the expression to pythons eval function; because of this, you can test your expression in python. You can run python code online here:

https://www.w3schools.com/python/trypython.asp?filename=demo_default

First import the math library, it has a lot of the math function you can call: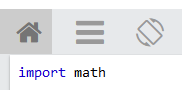

Now to simulate the tagId, you can declare variables to hold the reading from your tags like this:

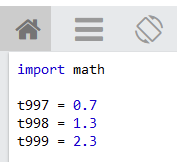
Next you can see the result of your expression by writing it in a print function like this (round is a built in function and floor is a function in the math library):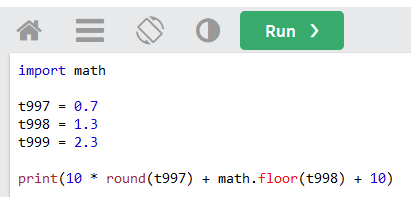

Click the Run button:

And see the result of your expression:

It properly seems confusing to see the floor function called as math.floor on the web site and it called as floor in the expression of calculated input. It is because the math library is included in the calculated input and will be searched when a function is called. This means that you don't have to worry about whether the function is builtin or a math library function, you just type the name of the function in the expression.

In python the function are located here:

Function	Python Location
acos	math library
asin	math library
atan	math library
atan2	math library
ceil	math library
cos	math library
cosh	math library
exp	math library
fabs	math library
floor	math library
log	math library
log10	math library
sin	math library
sinh	math library
sqrt	math library
tan	math library
tanh	math library
bool	built in function
int	built in function
round	built in function
random	Random library
omega	Not a Python function

Underlying lexer and parser rules

/*
 * Parser Rules
 */

evaluate 
	: expression EOF
	;
expression
	:  high_op_expression
	|  expression (OP_LOWER | BIN_OR_UN) high_op_expression
	;
high_op_expression
	:  temp_expression
	|  high_op_expression OP_HIGH temp_expression
	;
temp_expression
	:  brackets
	|  function_call 
	|  un_op_with_brackets
	|  un_op_with_term
	|  terminal
	;
brackets
	: '(' expression ')'
	;
function_call
	:  FUNC '(' expression ')'
	;
un_op_with_brackets
	:  (UN_OP | BIN_OR_UN)+ '(' expression ')'
	;
un_op_with_term
	:  (UN_OP | BIN_OR_UN)+ terminal
	;
terminal
	:  NUMBER
	|  BOOLEAN
	|  TAG 
	;

/*
 * Lexer Rules
 */

OP_HIGH
	:  'and'
	|  '&'
	|  '*'
	|  '/'
	|  '^'
	;
OP_LOWER
	:  'or'
	|  '+'
	|  '|'
	;
BIN_OR_UN
	:  '-'
	;
UN_OP
	:  'not'
 	|  '~'
	;
TAG
	:  [tT][0-9]+
	;
NUMBER
	:   '0' ([xX] [0-9a-fA-F]+         ([lL]  | [eE] [+-]? [0-9]+)?
	|        [oO] [0-7]+                [lL]?
	|        [bB] [01]+                 [lL]?)
	| ([0-9]+ '.' [0-9]* | '.' [0-9]+)         ([eE] [+-]? [0-9]+)?       [jJ]?
	|  [0-9]+                          ([lL]  | [eE] [+-]? [0-9]+ [jJ]? | [jJ])?
	;
BOOLEAN
	:  'True'
	|  'False'
	;
FUNC
	:  'acos'| 'asin'| 'atan'| 'atan2'| 'ceil'| 'cos'
	|  'cosh'| 'exp'| 'fabs'| 'floor'| 'log'| 'log10'
        |  'sin'| 'sinh'| 'sqrt'| 'tan'| 'tanh'|'bool'
	|  'int'| 'round'| 'random'| 'omega'
	|  
	;
WHITESPACE          
	:  (' '|'\t')+ -> skip ;

Recommended setup.

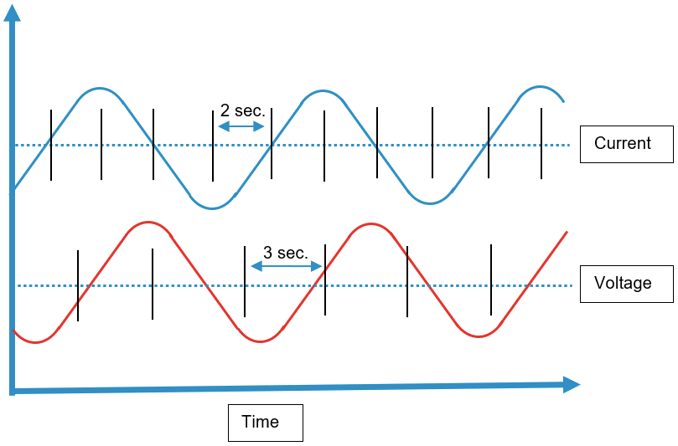
Combining the readings from several tags, can give behavior that seems strange, to avoid this you should set the scan rate of the calculated input and the tags used in the expression of the calculated input to the same value and the tags should come from the same PLC.

Scan rate should be the same for calculated input and tags used by it.
The tags used by the calculated input, should come from the same PLC.

Why the scan rate should be the same for calculated input and tags used by it

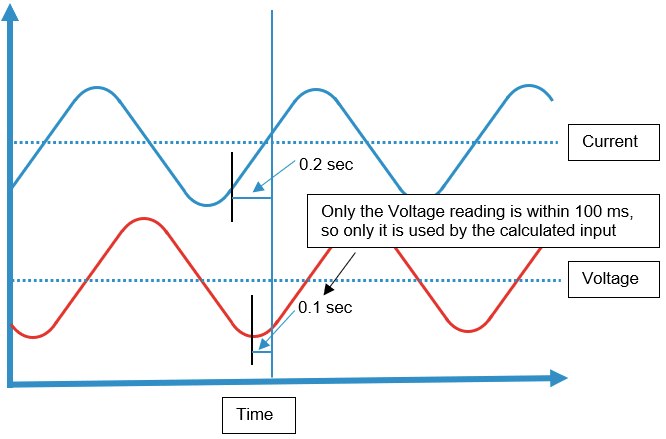
The reason why the scan rate should be the same, is because the calculated input has to use simultaneous values from the tags else the results can be incorrect. Imagine that you have a tag measuring current and other one measuring voltage. Now you want to calculate the power from these tags, you think "Simple, I just multiple them" after all the power formula is:

P(t) = U(t)* I(t)

And your current and voltage are waves:

And you scan your Current every 2 seconds and Voltage every 3 seconds:

Now image that we don't care when the scan happens and take values that are not simultaneous, then the question comes, which values do we pair with each other:

And even if we made a choice here, no matter which choice we take, the result would be wrong, because it the Current's value isn't neither of the choices, when we use a Voltage reading(This is also true, if we try paring from Current to Voltage):

And lastly, we must also take into account, when the calculated input is set to calculate the result via its scan rate, this also has to match the values from the tags. For example say that you set the scan rate of the calculated input to 5 seconds:

As you can see above, the calculated input toggles between having the Current and Voltage and therefore it isn't possible for it to make the calculation and as just explain before, we can't pair values that are not simultaneous.

The way we handle different scan rate on tags and calculated input, is to use the lowest common denominator for all of the scan rates. In the example before this would mean, that you would first get a result after 30 seconds, because that is the lowest common denominator between 2, 3 and 5. So if you want the results fast, when you have to think about setting their scan rate to the same or to something, where the common denominator is low enough for you.

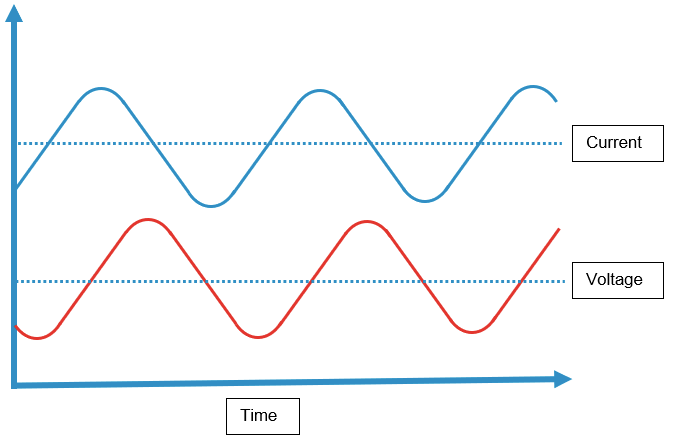
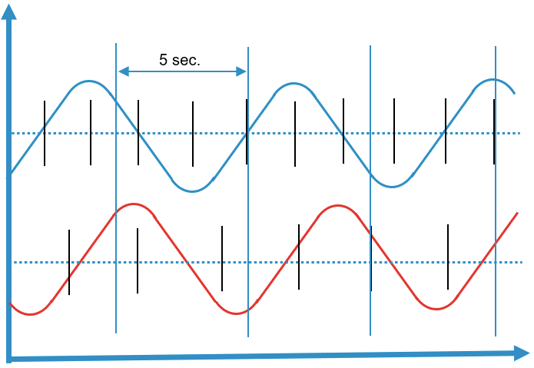
Why the tags used by the calculated input, should come from the same PLC

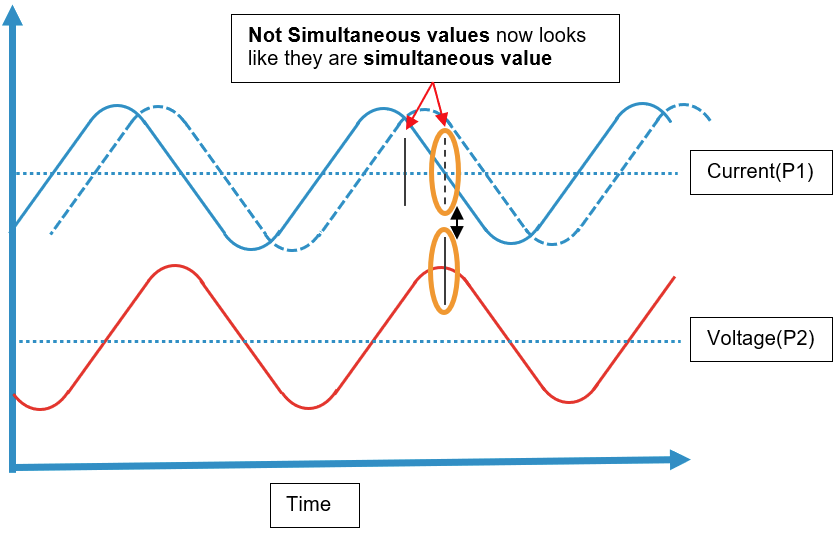
The reason why the tags used by the calculated input, should come from the same PLC, is because the clocks should be synchronized between the tags. Lets look at the Current and Voltage example, say that the Current tag is measured from PLC P1 and Voltage tag is measured from PLC P2:

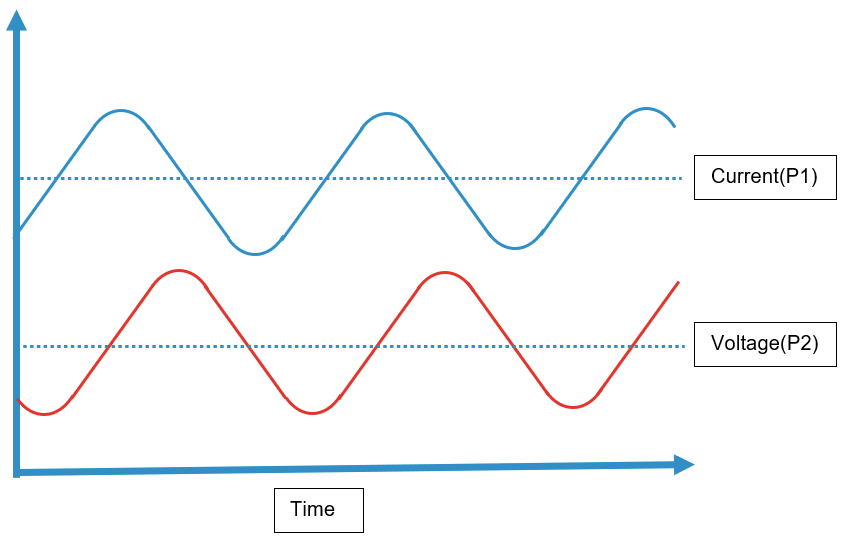
And image, that the clock on PLC P1 is 1 second late: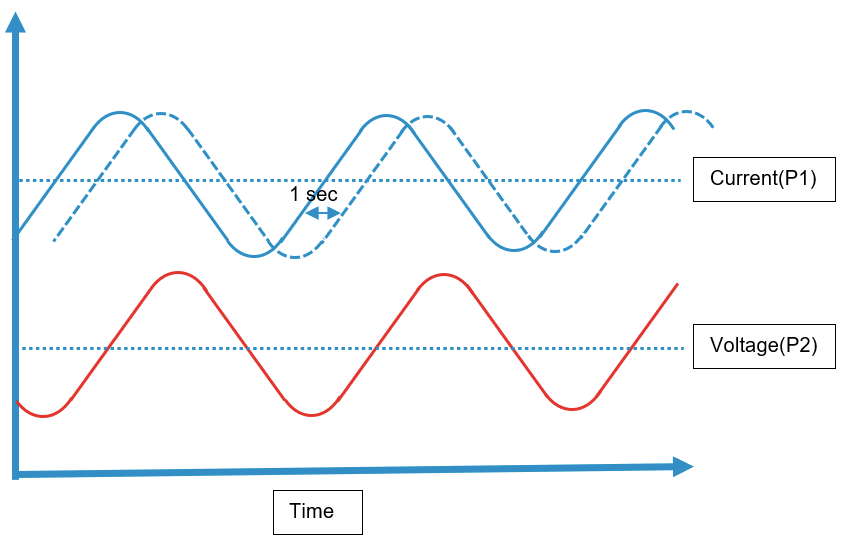

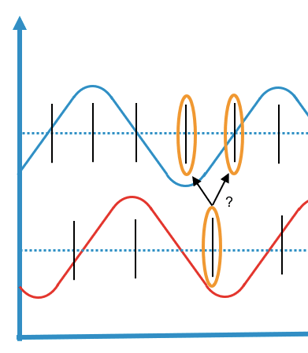
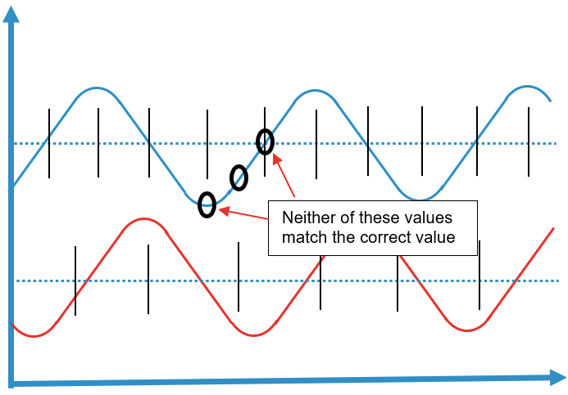
This can cause simultaneous values to appear not simultaneous, when the tags are read:

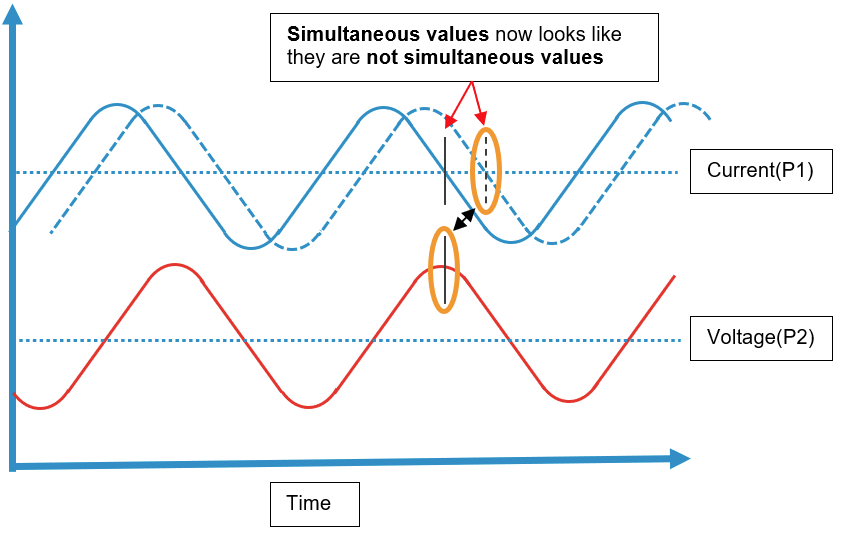
and not simultaneous values appear simultaneous, when the tags are read:

Tolerance on simultaneous values

Because clocks are not perfect synchronized with each other in the DIAP and PLCs, we have added a tolerance for when values between tags and calculated input are seen as simultaneous. This tolerance is 100 milliseconds, if tag's values are within 100 milliseconds of when they are read by the calculated input, then they are seen as simultaneous values and used by the calculated input: